Auf der folgenden Seite können einzelne Kacheln gedreht werden und erzeugen somit unterschiedliche Muster (html), imaginary.org.
Eine Mathematikseite ohne eine einzige Gleichung? Natürlich nicht.
\[ \pi = 4 - \frac{4}{3} + \frac{4}{5} - \frac{4}{7} + \frac{4}{9} - \frac{4}{11} \pm\, \ldots \] Ein erfrischender Zusammenhang von \(1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} \pm\, \ldots\) mit dem Verhältnis des Umfangs zum Durchmesser eines Kreises! Diese Darstellung soll bereits dem indischen Astronomen und Mathematiker Madhava aus Sangamagrama um 1400 bekannt gewesen sein (cf. storyofmathematics.com). Ebenfalls geht sie auf den schottischen Mathematiker James Gregory (cf. history.mcs.st-and.ac.uk), der sie 1671 John Collins mitteilte, zurück. Gottfried Wilhelm Leibniz hat sie 1682 veröffentlicht. Beweis über die Taylor/Maclaurin-Reihe (.html)/(.pdf). Zur Berechnung von \(\pi\) wird wie folgt notiert \[ \pi = 4 \cdot \sum_{n=0}^{\infty} \frac{(-1)^n}{2n+1}, \] \(n \in \mathbb{N}\). Um ein besseres Konvergenzverhalten zu erzielen, kann sie mit der Reihentransformation des Schweizer Mathematikers Leonhard Euler umgeschrieben werden zu \[ \pi=2\left(1 + \frac{1}{1\cdot3} + \frac{1\cdot2}{1\cdot3\cdot5} + \ldots + \frac{1\cdot2\cdots n}{1\cdot3\cdot5\cdots(2n+1)} + \ldots\right). \] Weiteres über die Zahl \(\pi\) findet sich auf 3.14...eu, joyofpi.com, piday.org oder z. B. pi314.net.
Die Formeln auf dieser Seite werden mit MathJax dargestellt. Selber Formeln erstellen?
MathJax \(\mathrm\LaTeX\)2HTML (.html) | \(\mathrm\LaTeX\)2SVG (.html) | KaTeX (.html)
Sitzt ein Kind auf einer Schaukel, wird es bald einmal versuchen auch «seitwärts» zu schaukeln. Auf einer alten Baumschaukel kann das ganz lustig werden. Systematisch untersucht haben orthogonale Schwingungen nachweisbar Nathaniel Bowditch und Jules Antoine Lissajous. Also, wenn man in einer englischen Enzyklopädie nachschaut, heissen die aus dieser Untersuchung entstehenden Figuren dort Bowditch-Kurven, in unseren Breiten werden sie indes durchwegs mit Lissajous verknüpft. Das Zeichnen von Schwingungen in zwei Raumdimensionen ist heute bestechend einfach realisierbar. Dem \(x\) und dem \(y\) wird einfach eine Sinusschwingung der Form \[ x = A\sin(at+\delta),\quad y = B\sin(bt) \] aufgebürdet und schon eröffnet sich ein auch ästhetisch weites Feld. Schwingen etwa beide Richtungen mit der gleichen Kreisfrequenz \(a = b\) und ist zudem \( \delta = \pi/2\), ergibt sich ein Kreis. Interessant wird es immer dann, wenn die Kreisfrequenzen Vielfache voneinander oder in einem rationalen Verhältnis zu einander sind oder beinahe...
Werden mehrere Schwingungen in beiden oder in einer Richtung ausgelöst, ergeben sich zuweilen verblüffend einfache, zum Teil aber auch ziemlich vertrackte Figuren. Diese können auch mechanisch mittels eines Harmonographen realisiert werden, cf. woodgears.ca oder karlsims.com. Nachfolgend eine Simulation dafür:
Interaktive Simulation eines Spirographen: desmos.com, (.svg); Inspirograph von N. Friend: nathanfriend.io
Setzt der Zeichenstift genau auf dem rotierenden Kreis an, entstehen Zykloiden (Epizykloiden: der Kreis rollt ausserhalb des fixierten Kreises ab, Hypozykloiden: innerhalb), sonst sind es Trochoiden (Epi- und Hypotrochoiden).
Erzeugen von kunstvollen Spirogrammen: github.com, (.svg)/(.pdf)/(.spiro), (.svg)/(.pdf)/(.spiro).
Zeichenmaschinen aller Art: drawingmachines.org
Das Zeichnen einer Rosette eignet sich vortrefflich für die Einführung von Polarkoordinaten \( (r,\theta) \) in Verbindung zu den kartesischen Koordinaten \( (x,y) = (r\cos(\theta), r\sin(\theta)) \), cf. (.svg) wikimedia.org. In Polarkoordinaten folgen die Rosetten einer besonders schlichten Vorschrift \[ r = \sin(n\cdot\theta), \] wobei \(n\) eine (natürliche) Zahl ist und \(\theta\) z. B. von 0 bis \(2\pi\) (360°) läuft. Dieser einfache Ausdruck, in kartesische Koordinaten übersetzt, winkt mit Rosen als Belohnung: (.html). Ist etwa \(n = \frac{3}{5}\) und \(u = 900\), ergibt sich (.svg), bei irrationalen Werten sind die Rosetten nicht mehr geschlossen, eine offene Rosettenbahn entsteht. Durch das Vergrössern der Schrittweite können bereits hier «Maurer-Rosetten» erzeugt werden, etwa für \(n=2\), \(u > 27\,720\) und Schrittweite \(92.4\) (.svg), \(27\,720 : 92.4 = 300\).
Ebene Polarkoordinaten sind nichts Schwieriges, sie öffnen im Gegenteil den Blick auf eine Welt, in der alles rund läuft. Die Bühne ist jetzt nicht mehr eine Gerade (\(x\)-Achse), sondern einfach der Ursprung \(O\), von dem alle Punkte eines Graphen nun quasi im Kreis herum gezeichnet werden.
Um Maurer-Rosetten zu erzeugen, werden Punkte auf einer Rosette durch Strecken miteinander verbunden. Die so erhaltenen Polygonzüge zeigen in ihren Hüllkurven (Einhüllenden) zuweilen Figuren, welche jenen des Spirographen nicht nur ähneln, sondern ebenfalls mit Zykloiden/Trochoiden in Verbindung gebracht werden können. Im Gegensatz zu den weiter oben im Abschnitt «Rosetten» durch grosse Schrittweiten erzeugten Polygonzüge sind Maurer-Rosetten stets geschlossen.
Die von Peter M. Maurer 1987 vorgestellten Polygonzüge sind im deutschsprachigen Raum immer noch relativ wenig bekannt, Originalarbeit “A Rose Is a Rose...”, The American Mathematical Monthly, 94 (7), pp. 631–45, jstor.org. Rosetten selber hat Luigi Guido Grandi in seinem Werk «Flores Geometrici Ex Rhodonearum Et Cloeliarum Curvarum Descriptionibus Resultantes» 1728 untersucht, archive.org.
Eine Anzahl \(n\) Mäuse, welche an den \(n\) Ecken eines (regulären) Polygons liegen, werden jeweils in zyklischer Reihenfolge von der nächstliegenden Maus (im Gegenuhrzeigersinn) magisch angezogen und bewegen sich stets in Richtung «ihrer» Maus. Darüber hinaus beeinflussen sich die Mäuse nicht. Die Geschwindigkeit kann als proportional zum Abstand der Zielmaus gewählt werden, im klassischen Fall ist diese einfach konstant.
Wir kennen also den Anfangszustand des Systems (Positionen) und das Gesetz, nach dem das System seinen Zustand ändert (funktionale Beziehung zwischen den momentanen Positionen und den Geschwindigkeiten). Solche Probleme lassen sich besonders einfach numerisch durch das Euler-Verfahren lösen, welches im Prinzip für jedes Anfangswertproblem eines Systems von gewöhnlichen Differenzialgleichungen anwendbar ist. Die Konvergenz-Geschwindigkeit ist in diesem Fall unerheblich und daher ist das Verfahren nicht nur einfach vermittelbar, sondern auch dem Problem angemessen. Besonders anschaulich ist indessen eine numerische Simulation (des Euler-Verfahrens).
Lassen wir im Hintergrund eine Uhr ticken und legen fest, dass sich bei jedem Tick die Mäuse um eine Strecke ihrem Ziel zu bewegen, haben wir bereits eine diskretisierte Formulierung des Problems. Dieses lässt sich relativ einfach in einem Computer-Programm umsetzen. Dabei errechnet sich z. B. die Position der Maus 1 (abhängig von Maus 2) rekursiv mit \[\label{a}\tag{0} \vec r_{1_{k}}=\vec r_{1_{k-1}} + h(\vec r_{2_{k-1}} - \vec r_{1_{k-1}}), \] wobei der konstante Faktor \(h\) den Anteil der Verbindungsstrecke angibt, welcher in jedem Zeitschritt zurückzulegen ist. Für den klassischen Fall einer konstanten Schrittweite normieren wir einfach \[\label{a_norm}\tag{1} \vec r_{1_{k}}=\vec r_{1_{k-1}} + h\cfrac{(\vec r_{2_{k-1}} - \vec r_{1_{k-1}})}{|(\vec r_{2_{k-1}} - \vec r_{1_{k-1}})|}. \] Genauso wird in zyklischer Reihenfolge für alle anderen Paare verfahren und nach jedem Zeitschritt eine Verbindungsstrecke gezogen. Dies sieht etwa so aus:
Konvergenz beim Dreieck für \(h=0.05\) und \(k=1,\ldots, 200\) (.txt); beim letzten Bild sind die Mäuse z. T. diagonal verknüpft.
☛ Klassischer Fall mit äquidistanter Schrittweite (\(v=\mathrm{konst.}\)): gleichseitiges Dreieck (.svg)/(.pdf), kombiniert (.svg)/(.pdf), überlagert (.svg)/(.pdf); Quadrat (.svg)/(.pdf), (.svg)/(.pdf); reguläres Pentagon (.svg)/(.pdf), (.svg)/(.pdf)
☛ Kombinationen mit (\(v\ne\mathrm{konst.}\)): gleichseitiges Dreieck (.svg)/(.pdf), (.svg)/(.pdf), (.svg)/(.pdf)
☛ Achteck mit Diagonalverfolgungen (.svg)/(.pdf), (.svg)/(.pdf)
Es sieht so aus, als bewegten sich die Mäuse auf Spiralen. Ausgehend von einem regulären Polygon kann gezeigt werden, dass sich die Mäuse nach jedem Zeitschritt wieder auf einer verkleinerten und rotierten Version des Polygons befinden (was die Simulation bereits vermuten lässt (.svg); Gleichung \( (\ref{a}) \) würde einen Fehler sogar «regularisieren»). Es ist daher auch möglich, ähnliche Bilder aus durch Drehstreckung erzeugten Kopien des Polygons mit gleichem Polygonzentrum zu zeichnen:
Es handelt es sich um logarithmische Spiralen, deren Ecken kaum sichtbar sind. Ein Beweis findet sich auf did.mat.uni-bayreuth.de/(.pdf), wo gezeigt wird, dass der Winkel zwischen dem Ortsvektor und dem Geschwindigkeitsvektor (dem Steigungswinkel) konstant bleibt. Weiteres zur Spirale im Quadrat (.pdf)/(.html).
Insbesondere über die «Hundekurven» (Radiodrome) gibt die Ausgabe No. 95-06 der «Berichte über Mathematik und Unterricht» der ETH Auskunft ethz.ch (.pdf).
Die logarithmische Spirale wird besonders einfach in Polarkoordinaten durch die Gleichung \[ \quad r(\varphi) = a \mathrm{e}^{k\varphi} ,\quad a,\,k,\,\varphi \in \mathbb R \] beschrieben; ist \(k=0\), beschreibt die Gleichung einen Kreis mit Radius \(a\). Dieser Parameter \(k\) wird als Steigung der Spirale bezeichnet \[ k = \tan(\alpha)\quad \mathrm{mit} \quad\alpha \in \left] -\tfrac{\pi}{2},\tfrac{\pi}{2} \right[, \] wobei \(\alpha \) Steigungswinkel heisst. Ist dieser Winkel konstant, handelt es sich um eine logarithmische Spirale.
☛ Hier kann die Wirkungsweise der Parameter ausprobiert werden: (.html)
Wird die Gleichung der Spirale nach \(\varphi\) aufgelöst, zeigt sich der natürliche Logarithmus, nach dem die Spirale benannt ist \[ \varphi(r) = \frac {1}{k} \ln \left( \frac {r}{a} \right). \] Jakob Bernoulli nannte sie liebevoll «spira mirabilis» (wundersame Spirale), denn sie weist einige ganz einzigartige Eigenschaften auf und wird in natürlichen Phänomenen auf eindrückliche Weise sichtbar.
☛ Das Zeichnen der logarithmischen Spirale mit dem Zirkel, Bulletin VSMP No. 115, 2011, pp. 10-18: vsmp.ch (.pdf)
☛ Achtung, nicht alles Spiralförmige in der Natur wird am besten durch eine logarithmische Spirale beschrieben. So ist etwa in der Anordnung der Kerne einer Sonnenblume eher eine archimedische Spirale sichtbar, cf. Spirale ist nicht gleich Spirale! ptb.de (.pdf)
Die aussichtsreiche Funktionentheorie, welche erst der Algebra ihren Fundamentalsatz schenkt, schreckt oft etwas durch ihre Begrifflichkeiten ab. So beginnen die meisten Vorlesungen mit «holomorphen Funktionen», mit Funktionen also, welche ganz in der Welt der komplexen Zahlen leben, scheinbar nur etwas für Fortgeschrittene. Ein Einstieg auf Meereshöhe scheint der nötigen Vorkenntnisse wegen zu klippenreich. Doch beginnen wir vielleicht bildlich, mit konformen Abbildungen. Voraussetzen müssen wir eigentlich nur, dass ein Punkt \( (x,y) \) in der Ebene vom Ursprung aus genauso durch seine Entfernung \(r\) und seine Peilrichtung, Winkel \(\varphi\), bestimmt werden kann: den Polarkoordinaten \( (r,\varphi) \), wobei \( (x,y) = (r\cos(\varphi), r\sin(\varphi)) \), cf. (.svg) wikimedia.org.
Konforme Abbildungen zeichnen sich durch die Eigenschaft aus, winkeltreu zu sein. Treue zahlt sich bekanntlich oft aus: unterwerfen wir ihnen regelmässige Polygonnetze, werden wir mit verblüffenden Formen belohnt, die dem Ausgangsmuster aber immer noch ähneln und wohl darum ihre Ästhetik bewahren. Ein Hexagonnetz (.pdf)/(.pdf) wird unter \(f(z) = z^2\), mit \(z = x + \mathrm i y\) und einer anschliessenden Drehung um −90° zu der Figur, welche das Eingangsbild zu diesem Eintrag zeigt, hier eine Version mit Krümmung (feinere Interpolation) (.pdf). Durch das Überlagern entsteht eine Würfelillusion, eine Art Kippbild. Wird das Netz allerdings nur um eine halbe Seitenlänge eines Hexagons verschoben, erhalten wir eine deckungsgleiche Überlagerung (.pdf).
Warum eigentlich diese Überlagerung? Das Quadrieren einer komplexen Zahl bewirkt neben der Quadratur des Betrages eine Verdopplung des Winkels, denn das Quadrat errechnet sich mit \[ z = x + \mathrm i y = r \cos(\varphi) + \mathrm i\,r \sin(\varphi) = r\bigl(\cos(\varphi) + \mathrm i \sin(\varphi)\bigr) = r\,\exp(\mathrm i \varphi) = r\,\mathrm{e}^{\mathrm i \varphi} \] zu \[ z^2 = (r\,\mathrm e^{\mathrm i \varphi})^2 = r^2 \mathrm{e}^{\mathrm i\,2\varphi}. \] Liegt der Punkt speziell auf dem Einheitskreis, wird nur diese Verdopplung sichtbar. Punkte im Inneren des Einheitskreises werden zum Nullpunkt hin verzogen, ausserhalb ergibt sich schnell eine Reise weit weg vom Zentrum. Der Nullpunkt ist übrigens bei dieser Funktion der einzige, welcher die Winkeltreue verletzt. Das Zeichnen solcher Abbildungen macht schnell einige der wichtigen Eigenschaften komplexwertiger Abbildungen spielerisch sichtbar.
Das verwendete Hexagonnetz kam in einer rechteckigen Form daher. Wir sehen, dass diese unter \(z^2\) in ein Zweieck verwandelt wird. Was passiert z. B. mit einer Dreiecksform (.svg), zentriert im Schwerpunkt? Wir sehen (.svg), es bleibt ein Dreieck, welches um 45° im Gegenuhrzeigersinn gedreht ist und von der Form her wie drei überlagerte Hinkelsteine aussieht, die sich hier nur gegen das Zentrum überschneiden (bei \(f(z) = z^3\) ergäbe sich nur ein Hinkelstein, warum?).
Besonders aufschlussreich scheint mir das Spielen mit der Exponentialfunktion \(f(z) = \exp(z)\). Aus einem einfachen zentrierten Quadratgitter (.svg) macht sie ein Netz, das geschlossen wird, sofern wir die Länge des Gitters mit einem Faktor auf \(2\pi\) skalieren: (.pdf). Eine Strahlen-Kreise Maschine: die rechte Seite der Quadratform verwandelt sich in den äussersten Kreis, die linke in den winzigen Innenkreis. Alle dazwischenliegenden Kreise entstehen durch Parallelen zur imaginären Achse, die radialen Halbgeraden (Strahlen) durch Parallelen zur reellen Achse.
Selber probieren? mathematikalpha.de
Hexagonnetz unter \(\exp(z)\) (.pdf), \(\sin(z)\) (.pdf), wieder um eine halbe Seitenlänge verschoben (.pdf), Dreieckgitter, diesmal im Quadrat zentriert, \(f(z) = \sin(z)\) (.pdf), Verfolgungskurven im Quadrat ebenfalls unter \(\sin(z)\) (.pdf).
Komplexe Funktionen können nicht vollständig visualisiert werden, es gibt aber Tricks, ihnen den einen oder anderen Aspekt abzuluchsen. Neben den hier vorgestellten konformen Abbildugen gibt es weitere, etwa Vektorfelder, die Riemannsche Zahlenkugel oder Phasenportraits. Eine Einführung durch Letztere in komplexe Funktionen gibt Elias Wegert in seinem Buch «Visual Complex Functions» springer.com 2012, researchgate.net. Siehe auch das interaktive Buch von Juan Carlos Ponce Campuzano complex-analysis.com, zum Spielen: brandonpelfrey.github.io (beachte, dass dort z. B. \(\sqrt{z}\) mit \(z^2\) vertauscht ist).
Konforme Abbildungen sind in Vorlesungen zur Funktionentheorie oft nur ein Randthema. Eine gewinnende Einführung bietet das thematisch erstaunlich breite Buch von Erwin Kreyszig: «Advanced engineering mathematics» (.pdf); wiley.com, welches sich über Jahrzehnte als Standardwerk gehalten hat.
L-Systeme verbinden Mathematik und Grafik auf eindrucksvolle Weise miteinander. Einfache Vorschriften führen oft zu komplexen Ergebnissen. Sie erlauben es Strukturen in der Natur zu modellieren und geben damit ein vereinfachtes Verständnis z. B. baumartiger Gebilde (Dendriten) oder Lichtenbergscher Figuren, cf. en.wikipedia.org. Aber auch andere, rekursiv definierte (selbstähnliche) Figuren lassen sich durch L-Systeme elegant produzieren.
Dabei ist zu beachten, das verwendete Alphabet eines L-Systems genau zu kennzeichnen. Als Beispiel diene, in Anlehnung an die bekanntere Koch-Schneeflocke/Insel (.svg), eine Art «Koch-Stern» mit dem Alphabet und den Ersetzungsregeln (.txt). Ordnung 0 (Axiom) bis 3:
Ordnung 4: (.svg)/(.pdf)/(.txt), Ordnung 5: (.svg)/(.pdf)/(.txt), Ordnung 6: (.svg)/(.pdf)/(.txt)
Beispiel mit Speicherung der Position (.svg)/(.pdf)/(.txt), ein schon fast legendärer Baum aus P. Prusinkiewicz and A. Lindenmayer «The Algorithmic Beauty of Plants», S. 25, Abb. 1.24e, mit den Regeln: (.txt), cf. algorithmicbotany.org.
Einfaches Python-Programm zur Erzeugung dieser Grafiken ☛ (.py) mit Ersetzungsregeln (.txt), weitere Grafiken ☛ (.html)
Figuren, welche durch Lindenmayer-Systeme erzeugt werden, sind selbstähnlich, sofern keine Skalierungen und Zufallsfaktoren ins Spiel kommen. Es sind auch Fraktale, doch was charakterisiert diese? «Fraktal» oder «gebrochen» meint eine rauhe, gewissermassen auslaufende Begrenzung. Diese findet sich in der Natur fast immer. Um diese Rauheit zu charakteriesieren, wird eine Zahl definiert, die Dimension eines Fraktals. Aber ist das wirklich eine Dimension wie eine Fläche oder ein Volumen?
Folgendes Dreieck wird durch eine zentrische Streckung um den Faktor 3 vergössert, skaliert. Wir sehen, dass neun des ursprünglichen Dreiecks in das vergrösserte passen:
Würden wir einen Würfel der Länge \(l\) mit dem Faktor \(k = 3\) skalieren, könnten wir \(N = 27\) des ursprünglichen in den vergrösserten Würfel packen. Das heisst wir definieren \(d\) durch \[ N = k^d\quad \Rightarrow \quad \boxed{d = \frac{\log N}{\log k}} = \log_k N. \]
Beim Würfel ist \(d\) gleich 3, ein Volumen. Für das Dreieck ist \(k = 3\) und \(N = 9\), woraus \(d = 2\) folgt, eine Fläche. Nun gut, das wussten wir schon. Die Gleichung erlaubt aber allgemein, eine «Dimension» zu bestimmen. Stellen wir uns vor, wir schneiden die grauen Dreiecke aus und rechnen jetzt mit \(k = 3\) und \(N = 6\). Wir erhalten mit \[ d = \frac{\log 6}{\log 3} \approx 1.631 \] eine irrationale, «fraktale» Dimension. Beim Sierpinski Dreieck, welches den Titel dieser Mathematikseite schmückt, ist es, wenn man sich die weissen Dreiecke ausgeschnitten denkt, \(\log_2 3 \approx 1.585\). Es gibt noch andere für die Praxis vorteilhaftere Definitionen. Wenn etwa die fraktale Dimension einer Küstenlinie bestimmt wird, welche nicht selbstähnlich ist, wird mit einem Gitter gearbeitet, um zu schauen, wie viel «ausgeschnitten» wurde, cf. de.wikipedia.org. Interesse geweckt? Ein immer noch profundes Buch, welches nur aus Vorworten besteht, ist jenes von Benoît B. Mandelbrot: «Die fraktale Geometrie der Natur», Birkhäuser Verlag, Basel 1987. Kurs über Fraktale der Universität, an der Mandelbrot lehrte math.yale.edu.
☛ Ein verwandtes Thema: Phyllotaxis (Applikation) (.html), cf. «The Algorithmic Beauty of Plants», S. 99ff.
Eine affine Abbildung, welche via
\[
\vec y = A\cdot \vec x + \vec t
\]
dem Ortsvektor \(\vec y\) einen neuen Ortsvektor \(\vec x\) zuordnet, kann eine ganze Menge, etwa verschieben, skalieren, scheren und/oder drehen! Dabei ist \(\vec t\) ein Verschiebungsvektor und \(A\) für die Zeichenebene eine \(2\times2\)-Matrix, welche \(\det A\neq 0\) erfüllt, womit eine bijektive Abbildung gegeben ist. Konkreter sieht das etwa so aus
\[
\begin{pmatrix}y_1 \\ y_2\end{pmatrix} =\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}\begin{pmatrix}x_1 \\ x_2\end{pmatrix} + \begin{pmatrix}t_1 \\ t_2\end{pmatrix}.
\]
Um zu zeigen, wie diese Transformation auf ein Objekt wirkt, sind skalierbare Vektorgrafiken (SVG) gut geeignet. Der Begriff «Vektor» ist irreführend, nicht nur der fehlenden Raumgeometrie wegen, sondern weil es sich hier vor allem um Pfadgrafiken handelt. Sie sollten eigentlich SPG heissen. Aber immerhin, auf Matrizen trifft man dort sehr schnell und man kann sie sogar sehen. Unsere Transformation wird in SVG mit transform="matrix(a11 a12 a21 a22 t1 t2)" erreicht. Nehmen wir einen schlichten Pfeil als Objekt:
Zuerst drehen wir den Pfeil um 30° und verschieben ihn etwas mit matrix(0.866 -0.5 0.5 0.866 -2 40):
Eine Drehung wird immer um den Ursprung \(O\) vollzogen. Der Pfeil würde also ohne Verschiebung nach oben aus dem sichtbaren Bereich «laufen». Diese vertikale Verschiebung ist der letzte Eintrag, es geht um 40 Pixel nach unten, das ist ein positiver Wert, da die Ordinate positiv nach unten zeigt. Auch beginnt der Pfeilschaft nicht genau in \(O\), somit muss auch noch ein wenig mit \(-2\) nach links verschoben werden. Solche Verschiebungen sind übrigens auch durch die geniale viewBox(t1 t2 Breite Höhe) ausführbar.
Schauen wir noch, was die matrix(0.75 0.1 -0.5 1.25 4 -5.25) bewirkt:
Das ist nun bereits eine Scherung, Verschiebung, Skalierung und Drehung in einem. Natürlich werden solche Transformationen meistens nicht händisch ausgeführt. Um jedoch die Arbeitsweise eines Zeichnungsprogrammes zu verstehen und damit genau arbeiten zu können, ist die Vertrautheit zu diesen Transformationsvorschriften überaus wertvoll.
Anstelle einer Matrix können die Transformationen auch direkt (und in Kombination) angegeben werden. So etwa eine Drehung um 30° durch transform="rotate(30)". Wir bleiben damit zur Freude Platons im Reich der rationalen Zahlen. Erst im Browser wird nun in der entsprechenden Drehmatrix cos(30°) je nach irdischer Genauigkeit berechnet und dargestellt.
\[ x^2 = x + 3 \quad\Leftrightarrow\quad \left(x - \frac{1}{2}\right)^2 = \frac{13}{4} \quad\Rightarrow\quad x_{1,2} = \frac{1\pm\sqrt{13}}{2}\approx \begin{cases}+2.302775637732 \\ -1.302775637732\end{cases}\; ; \] zugehörige Parabel: (.svg). Beim Quadrieren der positiven Lösung bleiben einfach alle Dezimalstellen unverändert stehen! Es gibt unendlich viele reelle Zahlen \(x\), für welche das Quadrieren mit der Addition einer natürlichen Zahl \(n\) endet: \(x^2 - x - n = 0\). Darunter finden sich auch einige Promis, etwa der Goldene Schnitt \(\Phi\), welcher sich um \(1\) erhöht, die \(2\), die sich gleich selber addiert und \(2\cdot2=2+2\) als Alleinstellungsmerkmal hätte, wäre da nicht die lichtscheue \(0\). Viele Menschen geben allzu viel auf (Zahlen-)Promis, was mir ganz fremd ist. Solche Promis zeigen sich in Alltagssituationen oft irdisch oder sogar unterirdisch. Die oben berechnete Zahl, wir könnten sie \(\Phi_3\) nennen, ist in diesem Zusammenhang genau so interessant wie \(\Phi_1\); sie addiert sogar mehr.
Welche Zahlen vermindern sich durch Quadrieren um \(3\)? Die zum Problem passende Parabel \(f(x) = x^2-x+3\) schneidet die \(x\)-Achse überhaupt nicht! Trotzdem, solche Zahlen \(z\) gibt es, sie leben in \(\mathbb{C}\), der Menge der komplexen Zahlen. Diese Zahlen \(z\) als geordnete Paare \((x, y)\) reeller Zahlen \(x\) und \(y\) zu betrachten, 1835 von William Rowan Hamilton eingeführt, ist konzeptionell äusserst gewinnend, wir identifizieren damit \(\mathbb{C}\) einfach mit \(\mathbb{R}^2\). Es braucht jetzt nur eine Addition zweier Zahlenpaare \[ (x, y) \oplus (u, v) := (x + u, y + v) \] mit einer Null \( (0,0) \) und eine geeignete Multiplikation \[ (x, y) \odot (u, v) := (xu -yv, xv + yu) \] mit dem Einselement \( (1,0) \) definiert zu werden. Aus \( (0,1) \odot (0,1) = (-1, 0) \) erhellt sich die Identifikation \( \mathrm i := (0, 1)\); also haben wir hier ganz natürlich \( \mathrm i^2 = -1\) gewonnen. Ist das nicht famos? Unser Problem \(z^2 - z + 3 = 0\) wird damit zu \[ (x^2-y^2, 2xy)-(x,y) + (3,0) = (0,0) \quad\Leftrightarrow \quad \begin{align*} x^2 -y^2-x+3 &=0\\ 2xy -y &=0\\ \end{align*} \] mit den Lösungen \(x = \frac{1}{2}\) und \(y = \pm\frac{\sqrt{11}}{2}\approx \pm1.658\). Quadrieren ergibt \[ z^2= \left(\frac{1}{2}, \pm\frac{\sqrt{11}}{2}\right)^2 = \left(\frac{1}{4}-\frac{11}{4}, \pm\frac{\sqrt{11}}{2}\right) \approx (-2.5, \pm1.658) = -2.5 \pm1.658\,\mathrm i. \] Der Imaginärteil \(\mathrm{Im}(z)=y\) bleibt beim Quadrieren unverändert, der Realteil \(\mathrm{Re}(z)=x\) vermindert sich wie gewünscht um drei. In \(\mathbb{C}\) finden zwar scheinbar utopische Probleme eine Lösung, wahr ist aber auch:
«Die Bezeichnung ‹imaginär› umgibt die komplexen Zahlen mit einer nicht zulässigen mysteriösen Aura. Mysteriös sind allenfalls die reellen Zahlen \(\mathbb{R}\), in \(\mathbb{C}\) leben bloss reelle Zahlenpaare mit ein wenig zusätzlicher Arithmetik.»
Das Inverse der Addition kann mit \( \ominus(x, y) := (-x, -y)\), das der Multiplikation für \( (x, y) \neq (0, 0) \) mit \( (x, y)^{\ominus 1} := (\frac{x}{x^2+y^2}, \frac{-y}{x^2+y^2})\) definiert werden. Damit lassen sich alle Eigenschaften zeigen, welche \( (\mathbb{R}^2, \oplus, \odot)\) zu einem Körper cf. de.wikipedia.org machen.
Zur Multiplikation: Mathematikerinnen suchen oft zu ihren Problemen eine geeignete Definition, die genau das macht, was sie möchten. Dann zeigen sie, dass die Definition in der Tat alle Anforderungen erfüllt. In diesem Fall hat Sir William auf seiner Suche nach Verallgemeinerungen der komplexen Zahlen wirklich ein goldenes Händchen gehabt.
Remmert, R. (1988). Komplexe Zahlen. In: Zahlen. Grundwissen Mathematik, vol 1. Springer, Berlin, Heidelberg, link.springer.com, S. 53ff.
D. L. macht in 60% seiner Handelsaktivitäten Verluste, nur in 40% ist er erfolgreich. Kann er trotzdem Geld verdienen? Sicher. Er muss nur schauen, dass bei den 40% systematisch mehr herausschaut. Schlüssel dazu ist, was in der Mathematik Erwartungswert heisst. Er erlaubt uns, was selten genug ist, eine der zahlreichen Börsenweisheiten quantitativ zu begründen: «Verluste begrenzen, Gewinne laufen lassen.»
Wenn D. L. pro Trade für den Kauf und Verkauf insgesamt CHF 12 zahlt und Verluste effektiv auf CHF 500 beschränkt, wie viel muss er dann im Erfolgsfall mindestens verdienen, damit der Gewinn \(g\) dem Verlust gerade die Waage hält? Aus der selbstredenden Gleichung \[ 0 = (-500 - 12)0.6 + (g - 12)0.4 \] folgt \(g = 780\); er muss also mindestens CHF 780 pro Gewinn-Trade verbuchen. Diese einfache Gleichung enthält vieles, was den meisten Menschen unendlich schwer fällt! Verluste begrenzen und realisieren ist hart, erfordert Konsequenz. Die Gebühren werden oft unterschätzt, summieren sich aber bei vielen Trades auf und immer zu Lasten! «Gewinne laufen lassen» (Stopps nachziehen) muss konsequent umgesetzt werden.
Der Erwartungswert ist ein durch die Wahrscheinlichkeiten gewichteter Durchschnittswert. Für Alltagsentscheide ist er eines der einfachsten aber auch mächtigsten Werkzeuge. Bereits Grundkenntnisse in Mathematik zahlen sich aus.
☛ Kreyszig, Erwin: Statistische Methoden und ihre Anwendungen. Vandenhoeck & Ruprecht 1973. ISBN: 3525407149. Kap. 6, Abschnitt 30.
☛ Erwartungswert de.wikipedia.org.
Der Rechenschieber ist wahrscheinlich das Instrument, welches der Ingenieurskunst am meisten Verbreitung gebracht hat. Er ist eine Art Taschenrechner unserer Grosseltern. Beim Aufstellen von Gleichungen der Art \(a=b^x\) und bei ihren Lösungen \(x\), den ominösen Logarithmen, geht der wundersame praktische Aspekt noch nicht auf: Multiplikation (Division) durch die leichtere Addition (Subtraktion) ersetzen! Die Berechnung einer Quadratwurzel reduziert sich auf eine Division durch 2.

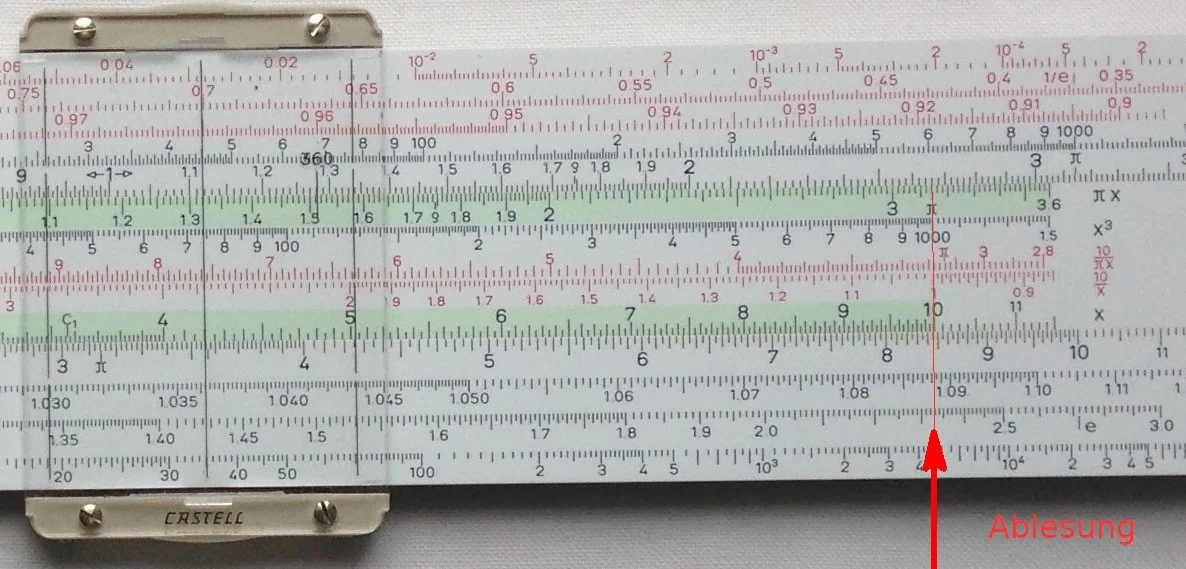
Faber Castell 2/82 N, hier eingestellt zur Berechnung von
\[
\sqrt[4.2]{35}\approx 2.33.
\]
Da lassen sich durchaus harte Nüsse knacken! Typischerweise liegen 3 signifikante Stellen drin.
Ein Rechenschieber zeigt diesen praktischen Aspekt und ist daher aus meiner Sicht von hohem didaktischen Wert, denn er erlaubt «händisches» Rechnen unter cleverer Verwendung grundlegender Zusammenhänge wie der Funktionalgleichung \[\label{fg}\tag{\(\star\)} \Phi(x\cdot y)=\Phi(x)+\Phi(y). \] Augustin Louis Cauchy hat 1821 gezeigt, dass die Lösungen dieser Funktionalgleichung definiert von \(\mathbb{R}^+\) nach \(\mathbb{R}\) genau die Logarithmusfunktionen \(\Phi(x) = \log_a(x)\) mit \(a\in\mathbb{R}^+\) sind. Sie werden somit durch die Eigenschaft, eine Multiplikation in eine Addition zu verwandeln, hergeleitet. Es wäre somit nicht abwegig, ausgehend vom Rechnen mit Potenzen, damit zu beginnen.
Auf der Seite rechenschieber.org findet sich eine ganze Auswahl von Anleitungen. Ein einfacher Rechenschieber kann mittels einer Kopiervorlage auch serienmässig gebastelt werden, wie etwa jener für eine «Lange Nacht der Mathematik» h-ka.de hergestellten math.kit.edu (.pdf).
Vermindert sich ein Wert \(W_0 = 100\) um \(2\,\%\) auf \(W_1=98\), muss er anschliessend um \(2.04\,\%\) steigen, um wieder den Wert 100 zu erreichen. Um diese Asymmetrie zu vermeiden und somit Modell-Rechnungen einfacher durchführen zu können, werden logarithmierte Renditen \[ \ln\left(\frac{W_1}{W_0}\right) = -\ln\left(\frac{W_0}{W_1}\right) = -\ln\left(\frac{100}{98}\right) \approx -2.02\,\% \] eingesetzt. Für kleine Renditen weicht die arithmetische von der logarithmierten Rendite nur wenig ab.
Es gilt die Additivitätseigenschaft von logarithmierten Renditen, d. h. diese Rendite ist gleich der Summe der Renditen über Teilzeiträume, eine direkte Folge von (\(\star\)).
In der Vorlesung «Mathematics for Computer Science» ocw.mit.edu (Lect. 13) gelingt Tom Leighton ein Hit mit der Frage, ob und wie gleiche Holzklötze gestapelt werden können, damit mindestens ein Klotz ganz über den Rand (Tischkante) ragt. Noch nie gehört, scheitern erste Versuche gewöhnlich, da intuitiv der Gebrauch von «rückwärts» stapeln sinnvoll erscheint. Solche Einführungen sind, wenn sie gelingen, stets besonders eindrücklich, denn sie erhöhen die Spannung auf die Auflösung im Nachgang enorm. Auch die Einführung in die Beweismethode der vollständigen Induktion (Lect. 2 & 3) ist in dieser Vorlesung sehr gelungen.
Im genannten Problem tauchen in der Lösung Partialsummen der harmonischen Reihe \[ \sum_{n=1}^\infty\frac{1}{n} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \cdots \] auf. Da diese Reihe divergiert, kann ein Klötzchen theoretisch (wenn genug davon vorhanden sind und die Stapelhöhe exorbitant werden kann) beliebig weit über den Tisch herausragen. Das ist immerhin ziemlich erstaunlich! Die Idee zur Realisierung dieser (nicht einzigen) Lösung ist eine «greedy strategy», womit der Bogen zur Programmierung elegant geschlossen wird. Illustration für 9 Klötzchen wikimedia.org.
Eine Inversion ist eine umkehrbare Abbildung, die mit ihrer Umkehrabbildung übereinstimmt. Bekannt sind vor allem die Punkt-, die Geraden- und die Kreisspiegelung (Inversion am Kreis) (.html), mathworld.wolfram.com.
Hier wird eine Quadratspiegelung vorgestellt. Analog zur Kreisspiegelung, wo \(r\) den Radius des Kreises, an dem gespiegelt wird, bezeichnet, soll gelten \[\label{aehnlich}\tag{$\star$} \overline{OP}\cdot\overline{OP'} = r^2, \] wobei \(r\) nun die variable Länge vom Ursprung zur Quadratseite ist, welche wir wie in der Abbildung mit dem Einheitsquadrat gleich 1 wählen.
☛ Simulation mit GeoGebra (.html), Abbildung einer Geraden (.html), eines Kreises (.html)
Wenn \(|y|\le|x|\) ist, haben wir \[ \frac{x'}{x}=\frac{\overline{OP'}}{\overline{OP}} \stackrel{(\ref{aehnlich})}{=}\frac{r^2}{\overline{OP}^2} =\frac{1}{\cos^2\varphi}\frac{\cos^2\varphi}{x^2} = \frac{1}{x^2} \] oder \[ x'=\frac{x}{x^2}, \;\ y' = \frac{y}{x^2} \] und falls \(|y|>|x|\) erhält man analog \[ x'=\frac{x}{y^2}, \;\ y' = \frac{y}{y^2}. \] Die so definierte Inversion am Quadrat ist keine konforme Abbildung, welche weiter oben kurz vorgestellt wurde, sie führt aber zu recht erstaunlichen Figuren, etwa von Strecken parallel zu zwei Quadratseiten (.svg)/(.pdf); Diagonale verwandeln sich in (.svg)/(.pdf). Ein Peano-Polygonzug (.svg) wird zu (.svg)/(.pdf) deformiert.
☛ Moiré-Effekt von Strahlen innerhalb eines Quadrates (.html), (.html); GeoGebra Animation (.html).
Zur Inversion am Kreis siehe auch das anschauliche Buch von Lorenz Halbeisen, Norbert Hungerbühler, Juan Läuchli: Mit harmonischen Verhältnissen zu Kegelschnitten. Springer Spektrum Berlin, Heidelberg. 2. Auflage 2021. link.springer.com, Kap 6.
Hier finden Sie Unterlagen zur Mathematik auf der Gymnasialstufe. Um die PDF Dokumente auszudrucken (oder elektronisch zu ergänzen) empfehle ich Ihnen den kostenlosen PDF XChange Viewer. Dieser wandelt beim Drucken unbekannte Zeichen in Pfade um, womit Probleme mit fehlenden Schriftsätzen entfallen.
☛ Die beste Investition im Übergang zum Studium: Durandi et al.: Formeln, Tabellen, Begriffe. ISBN 978-3-280-04193-2.